triangles constructeurs

géométrie sensorielle

Je sors,


je travaille,


Je range...

égal similaire équivalent

Géométrie avec mon p'tit coeur.
Concept d'égalité géométrique ... vous connaissez.

concept de similitude ... c'est moins évident que vous connaissiez en géométrie.
deux figures similaires ( même forme , pas même taille )

et là ... ça vous dit quelquechose ?


et bien c'est l'équivalence : même valeur de surface, mais pas la même forme.


regardez la première égalité, celle du rectangle, on le découpe et on obtient le triangle ! génial, non?

le vocabulaire de géométrie

Après avoir bien travaillé avec les nomenclatures sur le vocabulaire du carré, voilà comment l'enfant fait le synthèse ...






et la synthèse sur l'angle ...toute simple !


à partir de ma boite où se trouve le vocabulaire qui sert, biensûr, à d'autres figures !

comment obtenir une bonne mémorisation

Il y a une grande différence entre un tracé d'une ligne brisée et l'utilisation des barres de géométrie,

en utilisant les barres de géométrie, l'enfant vit avec ses sens la notion,

dans l'autre, il mémorise une notion déjà abstraite, qui peut s'éffacer plus facilement, et dont il ne peux vérifier ou retrouver par un seul "canal".

Quand l'enfant vit, il mémorise sur plusieurs canaux sensoriels.

mémoriser par répétition orale d'un théorème par exemple n'est pas aussi fiable que si vous dessinez la figure qui correspond à ce que vous voulez mémoriser.

et si vous débutez par une manipulation, vous vivez cette notion, vous l'inscrivez dans votre vie à un temps donné, et chacun de vos sens vous aide à mémoriser. Vos yeux qui voient , c'est une information dans votre cerveau, votre main qui touche s'en est une autre, votre langue qui dit le concept, en est une autre, votre oreille qui vous entend dire la notion encore une autre.

Vous avez "produit" de nombreuses connections dans votre cerveau. Ce sont ces liens qui donnent de la "solidité" à la mémoire. Ajoutez à cela une répétition de ces notions, afin que votre cerveau "retrouve facilement" le chemin, et un réel intérêt, c'est à dire une volonté d'apprendre, et vous obtenez les ingrédients d'une bonne mémorisation.

Donnons à nos enfants la joie de comprendre en apprenant, et d'apprendre en comprenant !

Aidons les à trouver les moyens de vivre concrètement, en faisant fonctionner leurs sens, au lieu de vivre virtuellement le savoir.

je viens de vous mettre en ligne comment faire les barres de géométrie ...

Maxime l'ovoïde et l'ellipsoïde

l'ovoïde et l'ellipsoïde ... cela vous paraît peut-être ressembler à deux gros mots à la capitaine Hadock ! Et bien non !

c'est le nom de la forme de l'oeuf (ovoïde) et du volume qu'on obtient en faisant la rotation d'une ellipse. Je ne dis biensûr rien de tout cela à Maxime !

Voilà mon fils prends les deux volumes et qui dit: "des oeufffs maman !"

Ah... voyons... ça ....et ça.... c'est pareil ?

OUUUiiiiiii !

Voyons ensemble, je vais faire le contour de cette forme. Avec le crayon rouge.
Puis je fais le contour aussi de celle la.

Maintenant, je retourne l'oeuf....attention "hop" (on le fait tourner d'un demi tour et on l'arrête)
On dessine encore, en rouge cette fois, le contour.

Avec l'ellipsoïde, on retrouve exactement le même tracé, mais pour l'ovoïde c'est différent.

Je pose chacun des dessins sous chacun des volumes et je redonne les noms de chacun des volumes. C'est " l'ellipsoïde" c'est "l'ovoïde"

Je demande "Montre moi l'ellipsoïde" .... - ....."Montre moi l'ovoïde" ....Max montre.

Je continue...ça rentre "comme dans du beurre" Il est dans la période sensible du langage.

"Qu'est ce que c'est ? " "l'ellipsoïde" (sourire des deux !) " Qu'est ce que c'est?" " l'ovoïde" Bravo ! allez, on range !

Nonnn ! Ah moi ! encore !

Je laisse Maxime et voilà ce qu'il fait (j'attrape discrètement l'appareil) :

je ne l'avais jamais vu découper autour d'une forme... c'est la première fois !

Je trouve ça génial !

Les angles

et je prépare... un petit plateau garni !

Je commence par... donner la notion d'angle.

Avec deux barres, "j'ouvre" un angle et je le "pose" sur une feuille, je dessine l'angle puis je demande à l'enfant d'en dessiner un lui aussi. Je vérifie que le vocabulaire est compris, et qu'il comprends la notation de la demi droite, qu'il a compris pourquoi on met telle ou telle lettre plûtot à droite ou à gauche dans la notation, si il a fait le lien avec le schéma.

Enfin, j'introduis la notation de l'angle, l'enfant passe de la manipulation concrète des barres de géométrie à la shématisation, et à force d'aller et retour, il trouve "plus simple" de faire le shéma directement,

ça y est, il est prêt ! :

J'ai ensuite appris à Marine à utiliser le rapporteur pour mesurer un angle. Elle m'a alors demandé ... si elle pouvait mesurer des deux cotés. Et voilà la notion d'angle complémentaires qui s'invite !

On en profite ! Marine a passé un petit moment à mesurer tous les angles dessinés ce matin puis à coté de chacun d'eux elle notait les valeurs de chaque angle, et la somme des deux angles !

En Montessori, pour l'éducateur, ces phases d'observation active de l'enfant en situation "réelle" sont essentielles pour arriver à une conscience de la progression de l'enfant. Je rappelle qu'il n'y a pas de plannification précise puisqu'on suit l'enfant dans son développement.

C'est vraiment important de respecter son rythme. De "foncer" quand il est motivé par une nouvelle découverte, de ralentir quand il y a des difficultés et de beaucoup l'observer dans ces moments là. Chaque enfant a son rythme propre ! Inutile de "forcer"...pour boucler le programme qu'on s'est fixé. Il faut de la souplesse, plus encore qu'avec la méthode classique, parce qu'on a comme objectif premier de respecter profondemment les lois de vie, et les spécificités de chaque enfant.

(C'est comme si on obligeait les enfants à grandir tant de cm par an, parce qu'on a établi un planning prévisionnel, pour connaitre quelle taille de chaussure acheter dans 6 mois, un an...et même dix ans !)

Enfin, il est important, pour que l'enfant soit toujours en confiance, qu'on ne le confronte pas à un test dès le début, puisque l'adulte peux voir cela dans la relation qu'il tisse avec l'enfant au moment de l'exercice. Et c'est de son devoir de prendre des notes ou marquer la progression d'une manière ou d'une autre afin de pouvoir noter la réelle progression de l'enfant, ou intervenir si l'enfant n'y arrive pas.

Je vois bien combien en ce domaine, je dois encore progresser ! Ce blog m'aide aussi à prendre conscience de mes pratiques.

On commence par les définitions d'angles particuliers par l'angle plat. Il y a beaucoup d'images vécues lors des initiations à la géométrie (premières leçons) qui reviennent comme un parallèle évident. Comme ici la surface du bocal d'eau que l'on a utilisé pour abordé la notion de droite horizontale.






Ensuite, voilà l'angle droit...la moitié d'un angle plat ! tout simplement ! et ses images vécues du fil à plomb qui plonge dans l'eau et la ficelle qui vient s'inscrire exactement à la verticale suivant une position "spéciale" !

Viens alors la présentation des autres angles :


L'angle obtu plus grand que l'angle droit !


Et l'angle aigu plus petit que l'angle droit !



Ensuite viens la présentation de l'angle nul.


"Eh HOP !, je ferme l'angle !"







"TOC !"" Il n'y a pas d'espace entre les deux demi-droites... on dit que les demi-droites sont confondues" . (Et on apporte le vocabulaire au fur et à mesure. )


"Voyons...peux tu mesurer l'angle qui est là" (on montre les deux barres superposées).


Dessinons le (et on montre comment dessiner en rappelant si besoin au passage les points sur lesquels l'enfant avait des difficultés précédemment).


Là, Marine me dit "Whaou !" celui là (elle montre l'angle complémentaire sur le dessin) je peux le mesurer ?


Et voilà qu'on obtient 0° + 360° = 360°


Et se retourne vers moi avec un sourire jusqu'aux oreilles ... je sais qu'elle est fière d'elle, et nous partageons en silence cette joie.



Belle journée !

Pour Marine cela représentait beaucoup de révisions. Les notions étaient connues et il s'agissait de faire émerger une vision d'ensemble.
Pour des notions nouvelles, et un enfant qui débute ... une à la fois c'est mieux, puisqu'en Montessori on présente toujours une nouveauté à la fois ! et une seule ! Puis des petits exercices d'application pour arriver en douceur à l'abstraction ( en laissant toujours le choix ... avec ou sans matériel ) On "attends" la maturité de la notion et le passage à l'abstraction par la répétition d'exercices similaires. Cela amène l'enfant à une "souplesse d'esprit" et à plus d'autonomie. (il se dit de plus en plus à lui-même sans aide du matériel ce qu'il doit faire et cela en toute confiance.

Ensuite Marine a travaillé à "créer sa leçon" avec les petits livret de la boite de nomenclature de géométrie . Avec son cours Pi, elle se fait sa propre synthèse. Ca donne ça !


Voilà ce sera tout pour aujourd'hui !

Pour faire vous-même vos barres de géométrie je vous donne le truc d'une amie... elle les a découpé dans des chemises plastiques, vous pouvez aussi faire dans du carton c'est plus "bio" mais moins solide.

Allez ! au travail !

les angles en 6ème - intro

Pour revoir les bases et se remettre en selle...rien ne vaut le concret !

Et justement, en géométrie c'est essentiel de savoir "visualiser" pour bien comprendre. Cette opération ne se fait pas si facilement que ça, et bon nombre d'enfants, une fois que l'on aborde les notations mathématiques, ne font plus le lien. Et ça donne des super salades mélangées de notions ! De confusion en confusion, ça devient difficile à rattraper !

Voilà ma boite de géométrie :




Voilà donc comment je procède avec Marine.

Ce matin au programme du cours pi, géométrie.Beaucoup de vocabulaire à revoir sur les angles. Je reprends donc mes barres de géométries, mon fichier Montessori (Merci Catherine qui a mis tout ça sur informatique, il n'y a plus qu'à découper ! plus de coloriages !)



Je reprends point par point ( c'est le cas de le dire !)

Tout d'abord, je rappelle rapidement en faisant le geste (sans rien dans les mains) de la droite.

Je la "pose" sur la feuille, et je tire un trait droit à cet endroit. "Donne-moi deux lettres de l'alphabet" "M et B" "ok, on appelle ta droite "(MB)" "tu vois c'est comme ça qu'on écrit quand c'est une droite" " deux lettres qui correspondent à deux points placés sur la droite, (et on place deux petits tirets sur la droite avec la lettre M et B sur chacun d'eux.)" (le point faisait l'objet d'une leçon antérieure) .



(pour ceux qui ne sont pas au courant, dans la présentation de la droite, on utilise deux bobines de ficelle du type cordeau de jardin qu'on déroule en la tendant bien, on déroule, on déroule des deux cotés avec les enfants pour "matérialiser" le fait qu'une droite n'a pas de fin, ...arrivée au mur on explique que ça continue en traversant tout, et la par l'imagination, on décrit ce qu'il y a derrière avec l'enfant en disant à chaque fois, "oui, oui la droite continue tout droit ! "et vous orientez votre droite de façon à ce qu'elle se dirige vers le soleil par exemple..."oui, oui, elle transperse le soleil, et elle continue", ... " et de l'autre coté ? " "-" "pareil ! oui, on traverse la terre, on arrive en Australie, ...on continue, on continue, etc". "une droite ça n'a pas de fin ni d'un coté , ni d'un autre, c'est pour cela qu'on l'appelle "infinie". Cette idée de tout traverser, les enfants adorent !

Et ils n'oublient plus la droite qui ne s'arrête jamais des deux cotés.)



Après la révision sur la droite, je refais le geste seulement de couper: "Eh couïc ! j'ai fait un trou dans ma droite, je "pose mes deux bouts sur la feuille" et je redonne la notation de la demi-droite donnant en dessin, puis, en notation : (MO] et [OB) . "je peux te faire une blague ?"
"Tiens ! ... voyons si tu peux mesurer la demi-droite ?" (en lui tendant une règle)
Eh NONNN! biensûr, une demi-droite, c'est toujours infini d'un coté, alors on ne peux pas mesurer ! Bravo, tu es drôlement malin !"

Et maintenant attention !
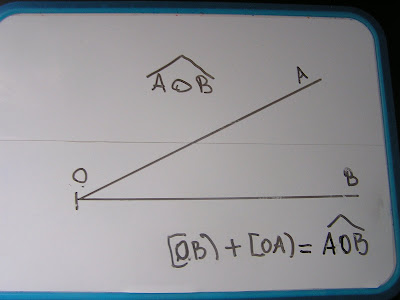
Et "couïc !" on passe au segment... et à sa notation : [OA].
Après on donne quelques exercices écrits sur ce thème (j'aime bien les livres LCR pour ça)

On continue... avec les barres de géométrie.

Mon ptit coeur et les surfaces

Voici un matériel pour travailler sur les surfaces en géométrie que Mon ptit coeur travaille tout d'abord en sensoriel c'est à dire en découverte individuelle... et surtout sans discours !



Silence on travaille !
Plus tard ce matériel sert à trouver les équivalences entre les différentes défintions sur les surfaces...
par exemple..."Quel rapport y a t'il entre les surfaces d'un rectangle d'un triangle rectangle et d'un rhombe (losange) "

mais ça ce n'est pas encore du niveau de Mon ptit coeur...attendons que Mon trésor en soit là et je vous montre !

PS : Les photos ont été prises par Mon ptit coeur !

découverte de la géométrie

Quel merveilleux outils que les nomenclatures montessori !



En organisant son savoir, l'enfant expérimente au fur et à mesure les notions proposée dans un ordre cohérent, une notion à la fois, petit à petit.


la notion de point,

c'est infiniment petit, un point, alors on fait tailler à l'enfant le crayon et il pose son minuscule point sur la feuille.
Alors, on s'exclame "Oh ! mais il est beaucoup trop gros, il faut tailler encore..." et on essaye ainsi de faire le plus petit point possible.
après quelques essais, on dit "tu vois, c'est tellement petit un point qu'on ne devrait même pas le voir !"


"..."

"tellement c'est petit, un point, alors on a decidé de faire une petite croix pour dire qu'il est ... là."

"comme un trésor ?" m'a demandé l'enfant

oui, comme un trésor, car en géométrie, on va tout construire avec des points, plein de points.


puis on le laisse lire la définition, et retrouver la carte qui va avec...


on continue, de la même manière la découverte de la notion de ligne...
"et si je décide de dessiner un autre point à coté du premier, et un autre, et un autre....qu'est ce que ça donnerait ...essaye de faire çà.
et l'enfant expérimente

géométrie (suite1)

de la même façon on introduit la ligne,


puis la surface plane...


-"et une "surface courbe" c'est comme ça ?" demande l'enfant ...


et enfin la notion de volume...


à chaque fois, on cherche dans la pièce à quoi ça correspond dans la réalité.

géométrie (suite2)

Mon ptit coeur lit les définitions et retrouve dans chacune des notions découvertes



elle rassemble toutes les découvertes...par la mise en paire image/définition


puis elle travaille les définitions à trou, l'enfant écrit sur une étiquette le nom de la notion effacée sur la définition et rassemble l'étiquette et la définition à trou correspondante.


Elle corrige avec la définition qu'elle retourne ensuite.
c'est le travail de mémorisation.


Et voilà...

géométrie (suite3)

Mon ptit coeur a ensuite créé son propre volume en papier
découpage...
La réalisation finie, elle est venue la poser naturellement à coté de l'étiquette "volume "!


et chaque notion est travaillée ainsi,
il y en a toute une boite !


Ensuite on a fait un petit jeu
ça s'appelle "les ordres de géométrie"
C'est un travail de lecture et une sorte de devinette
Là, Laura, petit à petit, a fait le lien entre point et unité,
barre de dix et ligne, plaque de 100 et surface, cube de 1000 et volume.
je vous laisse deviner ce que cela peut préparer sensoriellement...

Et voilà, on a commencé,
c'est la première pochette,
Et...il y a encore tout ça pour s'amuser !